Lección 4
Torque y equilibrio de un cuerpo rígido
En general un cuerpo puede tener tres tipos distintos de movimiento simultáneamente. De traslación a lo largo de una trayectoria, de rotación mientras se está trasladando, en este caso la rotación puede ser sobre un eje que pase por el cuerpo, y si a la vez este eje está girando en torno a un eje vertical, a la rotación del eje del cuerpo rotante se le llama movimiento de precesión (por ejemplo un trompo), y de vibración de cada parte del cuerpo mientras se traslada y gira. Por lo tanto el estudio del movimiento puede ser en general muy complejo, por esta razón se estudia cada movimiento en forma independiente.
Cuerpo rígido:
Se define como un cuerpo ideal cuyas partes (partículas que lo forman) tienen posiciones relativas fijas entre sí cuando se somete a fuerzas externas, es decir es no deformable. Con esta definición se elimina la posibilidad de que el objeto tenga movimiento de vibración. Este modelo de cuerpo rígido es muy útil en muchas situaciones en las cuales la deformación del objeto es despreciable.
El movimiento general de un cuerpo rígido es una combinación de movimiento de traslación y de rotación. Para hacer su descripción es conveniente estudiar en forma separada esos dos movimientos.
Torque de una fuerza
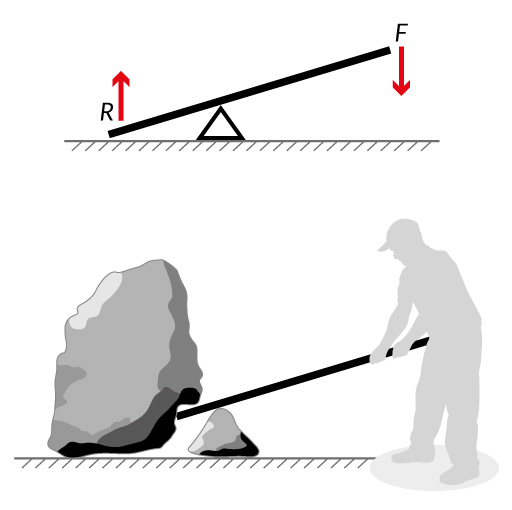
Cuando se aplica una fuerza en algún punto de un cuerpo rígido, el cuerpo tiende a realizar un movimiento de rotación en torno a algún eje. La propiedad de la fuerza para hacer girar al cuerpo se mide con una magnitud física que llamamos torque o momento de la fuerza.
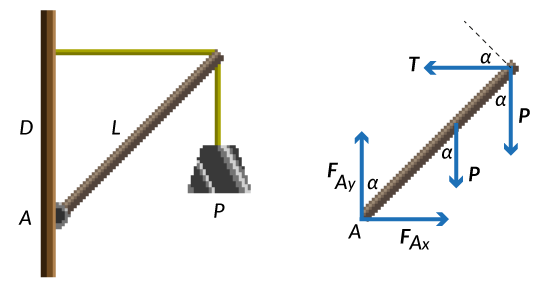
Se define el torque τ de una fuerza F que actúa sobre algún punto del cuerpo rígido, en una posición r respecto de cualquier origen O, por el que puede pasar un eje sobre el cual se produce la rotación del cuerpo rígido, al producto vectorial entre la posición r y la fuerza aplicada F, por la siguiente expresión:
El torque es una magnitud vectorial, si α es el ángulo entre r y F, su valor numérico, por definición del producto vectorial, es:
`tau = r(Fsenalpha)`Por convención se considera el torque positivo (negativo) si la rotación que produciría la fuerza es en sentido antihorario (horario). La unidad de medida del torque en el SI es el Nm (igual que para trabajo, pero no se llama joule).
Equilibrio de un cuerpo rígido
Por definición una partícula puede tener solo movimiento de traslación. Si la resultante de las fuerzas que actúan sobre una partícula es cero, la partícula está moviéndose con velocidad constante o está en reposo; en este último caso se dice que está en equilibrio estático.
Pero el movimiento de un cuerpo rígido en general es de traslación y de rotación. En este caso, si la resultante tanto de las fuerzas como de los torques que actúan sobre el cuerpo rígido es cero, este no tendrá aceleración lineal ni aceleración angular, y si está en reposo, estará en equilibrio estático.
Para que un cuerpo rígido este en equilibrio estático se deben cumplir dos requisitos simultáneamente, llamados condiciones de equilibrio:
`sum bar F = 0` ; Primera condición de equilibrio`sum bar tau = 0` ; Segunda condición de equilibrio
Actividades de aprendizaje
Bibliografía
- Wilson, Jerry D. Física. Segunda edición. Ed. Pearson Educación. 1996. ISBN 968-880-660-9
- Serway, Raymond y Jewet, John. Física I. Tercera edición. Texto basado en Cálculo. Ed. Thomson. 2004. ISBN 970-686-339-7
- Sears, Zemansky, Young, Fredman. Física Universitaria. Undécima edición.Person Ed.