Para abordar el problema fundamental de la física, que radica en la posibilidad de describir cómo será el movimiento de los cuerpos, teniendo conocimiento de todas las fuerzas que afectan el sistema, se necesita retomar la aplicación en su desarrollo de la segunda Ley de Newton, pero si se considera que las fuerzas no son constantes, podríamos toparnos con la sorpresa que la aceleración, tampoco lo es, entonces, hallar la velocidad del cuerpo y su posición, no sería fácil una tarea fácil.

Los conceptos de trabajo y energía son de gran importancia tanto en la ciencia como en la vida cotidiana. No incluyen conceptos adicionales, todo está fundamentado en las Leyes de Newton. Convirtiéndose en un método alternativo para describir el movimiento cuando las fuerzas no son constantes.

Así mismo, considerar otras aplicaciones de los conceptos en la parte del estudio del equilibrio de un cuerpo rígido

Para reflexionar:

1. ¿Porqué el trabajo realizado por la fuerza de rozamiento debida al deslizamiento es negativo cuando un objeto se somete a un desplazamiento sobre una superficie rugosa?
2. ¿Puede ser negativa la energía cinética?
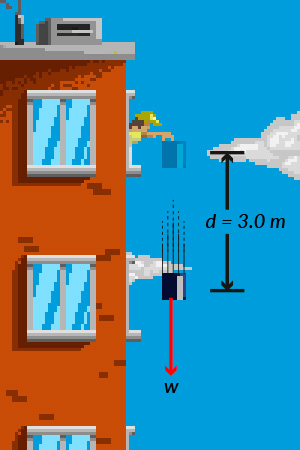
3. A menudo, cuando un clavadista quiere girar en el aire, junta las piernas contra su pecho. ¿Por qué esto hace que gire más rápido? Qué debería hacer cuando quiera dejar de girar?

La energía existe en varias formas: hay energía mecánica, energía química, energía eléctrica, energía térmica, energía nuclear y demás. Puede haber alguna transformación de una forma de energía a otra pero la cantidad total de energía se conserva, es decir, siempre permanece igual.

Trabajo realizado por una fuerza constante

La palabra trabajo se utiliza comúnmente en una diversidad de formas: vamos al trabajo; trabajamos sobre proyectos; trabajamos en problemas. Sin embargo, en física, trabajo tiene un significado muy específico. Mecánicamente, trabajo comprende fuerza y desplazamiento, y se usa este trabajo para describir cuantitativamente lo que se obtiene cuando una fuerza mueve un objeto a lo largo de una distancia.

En el caso más sencillo debido a una fuerza constante, se enuncia como:

Trabajo realizado por una fuerza constante al mover un objeto es igual al producto de las magnitudes del desplazamiento y los componentes de la fuerza paralela al desplazamiento.

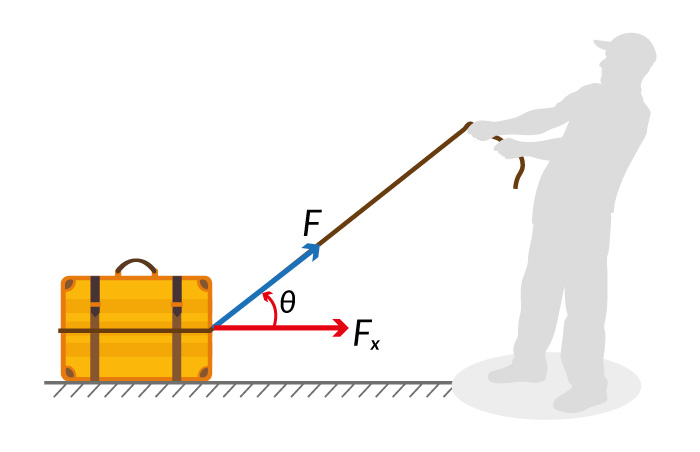
Entonces, para una fuerza constante F que actua en la misma dirección que el desplazamiento d, el trabajo (W) es:

`W = Fd`
`W = Fd = (Fcostheta)d = Fdcostheta`

Obsérvese que si `ɵ = 0°`, el trabajo será determinado por el producto entre `F` y `d`. El componente perpendicular de la fuerza, `F= Fsenɵ`, no realiza trabajo, dado que no hay desplazamiento en esa dirección. El ángulo `ɵ` es entre la fuerza y los vectores de desplazamiento. Si la fuerza actua en la dirección opuesta al desplazamiento (`ɵ = 180°`) el trabajo será negativo.

Trabajo debido a una fuerza constante

Ejemplo: El trabajo mecánico requiere movimiento

El trabajo es una magnitud escalar, en el SI el trabajo se considera como Nm, la unidad recibe el nombre de Joule (J).

Trabajo realizado por una fuerza variable

En general, las fuerzas son variables, esto es, cambian con el tiempo y/o la posición. Si una fuerza variable F está moviendo a un objeto a lo largo de un eje desde una posición inicial a otra final, ya no se puede usar la expresión anterior para calcular el trabajo realizado por la fuerza. En este caso puede decirse, que el cuerpo experimenta pequeños desplazamientos, y a su vez hablar que el componente de la fuerza en dirección al desplazamiento se puede considerar aproximadamente constante en ese intervalo.

Consideremos un ejemplo de fuerza variable que hace trabajo en un resorte que se estira. Conforme el resorte está estirado (o comprimido) cada vez más, la fuerza de restauración del resorte se hace más grande y es necesario aplicar una fuerza mayor. Se encuentra que la fuerza aplicada `F es directamente proporcional al desplazamiento o al cambio de longitud del resorte.

Esto se puede expresar en forma de ecuación:

O con `X_"0" = 0,`

Como se puede ver, la fuerza varía con `x`. Esto se describe diciendo que la fuerza es una función de la posición. La `K` en esta ecuación es una constante del resorte, elasticidad o de la fuerza. Mientras mayor sea el valor de `k`, más rígido o fuerte será el resorte. Las unidades de `k` son `(N/m).

Ejemplo: Fuerza del resorte

En el esquema se muestra:

1. Una fuerza `F` aplicada estira el resorte, y el resorte ejerce una fuerza igual y opuesta `F_"s"` sobre la mano.
2. La magnitud de la fuerza depende del cambio en la longitud del resorte. Con frecuencia se hace referencia a esto como posición de una masa en el extremo del resorte.

La relación expresada por la expresión anterior, se mantiene solo para los resortes ideales. Los resortes verdaderos se aproximan a esta relación lineal entre fuerza y desplazamiento, dentro de ciertos límites. Se observa que el resorte ejerce en realidad una fuerza igual y opuesta, `F_"s"= - kΔx`, cuando su longitud lineal cambia en una magnitud `Δx`. El signo negativo indica que la fuerza del resorte está en dirección opuesta al desplazamiento si el resorte se estira o se comprime. Este principio se conoce como la Ley de Hooke.

Trabajo realizado por una fuerza que varia en forma uniforme

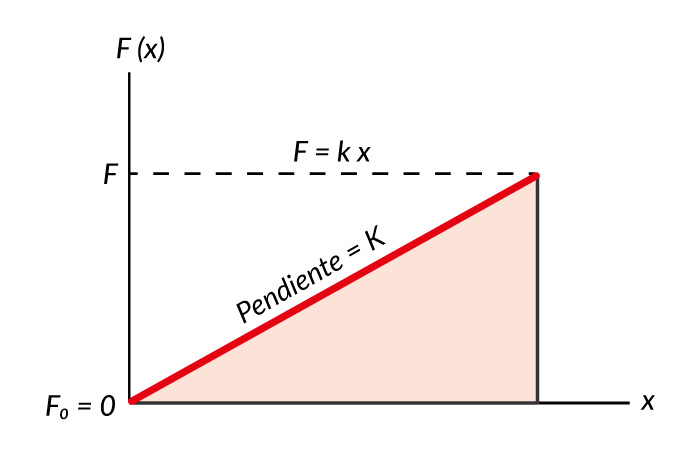
En la gráfica de `F` contra `x`, la pendiente de la línea es igual a `k`, y `F` se incrementa uniformemente con `x`. La fuerza promedio es entonces:

`bar F = (F + F_"0")/2`

O si `F_"0" = 0`

`bar F = F/2`

Así, el trabajo realizado al estirar o comprimir el resorte es

Como F=kx, el trabajo realizado es:

Teorema de Trabajo – Energía: Energía Cinética

Ahora que se tiene una definición operacional de trabajo, estamos listos para ver como se relaciona el trabajo con la energía. Energía es uno de los conceptos más unificadores en la ciencia. La describimos como una magnitud poseída por objetos y sistemas. Básicamente, el trabajo es algo que se realiza sobre los objetos, mientras que la energía es algo que los objetos tienen.

Con frecuencia se denomina energía cinetica a la energía del movimiento. Es definida matemáticamente como la mitad del producto de la masa y el cuadrado de la velocidad de un objeto.

Para una fuerza neta constante que realiza un trabajo sobre un objeto en movimiento, la fuerza realiza un `W=Fx`, el objeto se acelera:

Por segunda ley de Newton `F=ma` y sustituyendo entonces:

En términos de la energía cinética, entonces:

`W = 1/2mv^2 - 1/2mv^20 = K - K_"0" = DeltaK`
`W_"neto" = DeltaK`

Esta ecuación se llama teorema de trabajo-energía y relaciona el trabajo neto realizado sobre un objeto con el cambio en su energía cinética.

Ejemplo: Ejemplo de trabajo y energía cinética

Energía potencial

Un objeto en movimiento tiene energía cinética. Sin embargo, ya sea que un objeto esté o no en movimiento, puede tener otra forma de energía: energía potencial. Como su nombre lo indica, un objeto que tiene energía potencial tiene el potencial para realizar un trabajo. El potencial para realizar un trabajo se deriva de la posición o configuración de los cuerpos. En cierto sentido, se puede considerar que la energía potencial es trabajo almacenado.

Ejemplo: Energías potencial y cinéticas

Para eventos como la compresión de un resorte, o el trabajo que se hace en contra de la fuerza de gravedad, se puede enunciar lo siguiente:

`W = DeltaE_"p" = DeltaU = U - U_"0"`
`E_"potencial-resorte" = DeltaU = 1/2 Kx^2`
`E_"potencial-gravitacional" = DeltaU = mgh`