Para hablar de un movimiento bidimensional curvilíneo pensemos en un ejemplo en el cual se ven objetos lanzados o proyectados por algún medio. Cuando una piedra es lanzada través de una corriente. o en una pelota de béisbol cuando se realiza su lanzamiento. Ya se ha discutido movimientos en casos particulares como cuando es proyectado de manera vertical en el movimiento de caída libre.

Por lo general, se desprecia la resistencia del aire y solo se considera la aceleración debida a la gravedad que actúa sobre el proyectil.

De manera más sencilla, se analiza el movimiento de proyectil si se usan las componentes vectoriales. Solo entonces, se debe fraccionar el movimiento y observar sus componentes unidimensionales individuales.

Analicemos entonces el caso particular del movimiento de un objeto proyectado horizontalmente, o paralelo a una superficie plana.

Supongamos que se lanza un objeto horizontalmente con una velocidad inicial `v_"x0"`. El movimiento del proyectil se analiza a partir del instante en el cual es liberado `(t=0)`. Una vez el objeto es liberado, la aceleración horizontal es cero `(a_x=0)`, de modo que la velocidad horizontal es constante `v_x=v_"x0"`. Como ya sabemos que la posición es función de la velocidad y el tiempo, el objeto al ser proyectado podría viajar indefinidamente en la dirección horizontal. Sin embargo, esto no sucede, pues recordemos que tan pronto el objeto es proyectado, está en caída libre en dirección vertical, con `v_"y0" = 0` (como si soltara) y `a_y= -g`. El resultado es una trayectoria curva.

Nota:

En esencia, el objeto proyectado viaja con la misma velocidad uniforme en la dirección horizontal mientras que al mismo tiempo experimenta una aceleración hacia abajo, soportando la influencia de la gravedad. El resultado es una trayectoria curva. Si no hubiera el movimiento horizontal, el objeto caería sencillamente al suelo en una línea recta, y de hecho, el tiempo de vuelo del objeto lanzado es exactamente igual que si lo hiciera verticalmente (caída libre).

Proyecciones con ángulos arbitrarios

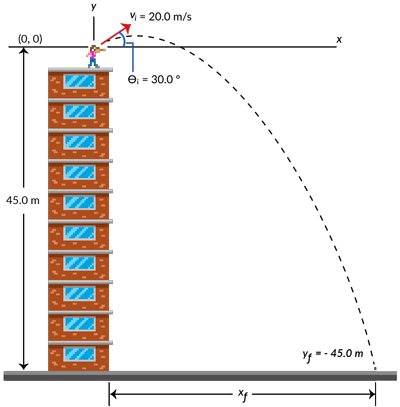
Como el movimiento del objeto proyectado describe una trayectoria curva, este debe tener al analizarse un ángulo `theta` arbitrario, en relación con la horizontal. Se analiza entonces, su comportamiento utilizando las componentes y la respectiva convención.

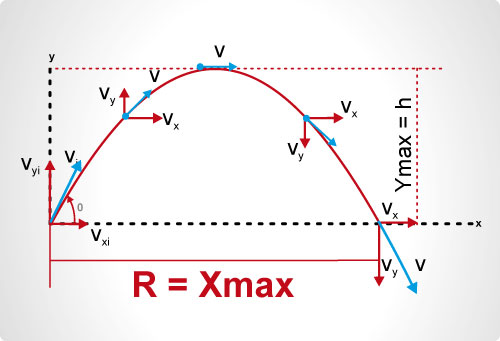
Primero, la velocidad inicial `v_0` se resuelve en sus componentes rectangulares:

Componentes de la velocidad inicial `(t=0)`

`v_"x0" = v_0 cos theta`

`v_"y0" = v_0 sin theta`

Dado que no hay aceleración horizontal y la gravedad actúa en la dirección y negativa, el componente `x` de la velocidad es constante y el componente `y` varía con el tiempo:

Componentes de la velocidad inicial `(t>0)`

`v_x = v_"x0" = v_0 cos theta`

`v_y = v_"y0" -g t = (v_0 sin theta) - g t`

En forma similar, las componentes del desplazamiento están dado por:

Componentes del desplazamiento

`x = v_"x0" t = (v_0 cos theta) t`

`y = v_"y0"t + 1/2 g t^2 = (v_0sin theta)t -1/2 g t^2`

Ejemplo: Vuelo de la piedra desde el edificio

En conclusión: la curva generada por estas ecuaciónes, o la trayectoria del movimiento del proyectil se llama una parábola.

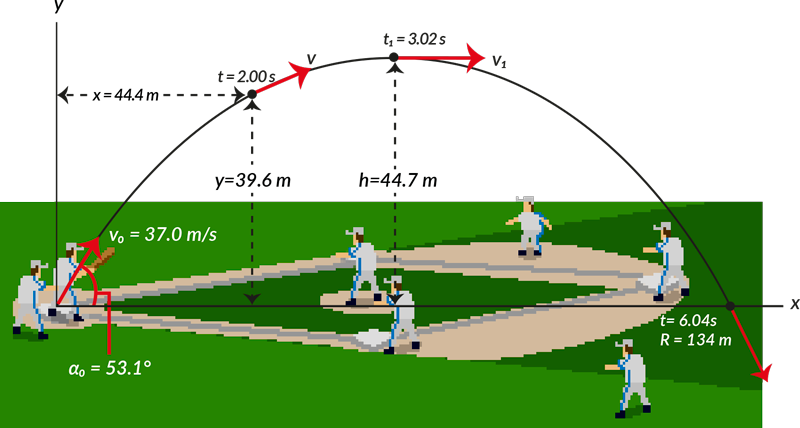
Algunos aspectos del movimiento de proyectil que pueden ser de interés en diversas ocasiones incluyen el tiempo de vuelo, la altura máxima alcanzada y el intervalo, que es la distancia horizontal máxima viajada.

Ejemplo: Distancia máxima movimiento de proyectil

Ejemplo: Movimiento de proyectil

Bibliografía

• Wilson, Jerry D. Física. Segunda edición. Ed. Pearson Educación. 1996. ISBN 968-880-660-9
• Serway , Raymond y Jewet, John. Física I. Tercera edición. Texto basado en Cálculo. Ed. Thomson. 2004. ISBN 970-686-339-7
• Sears, Zemansky, Young,Fredman. Fisica Universitaria. Undécima edición.Person Ed.