Lección 3
Movimiento en dos dimensiones
En esta lección estudiaremos la cinemática de los objetos cuando se mueven sobre dos dimensiones, dibujando trayectorias curvas, describiéndose a partir de las ecuaciones ya conocidas. El movimiento curvilíneo es muy fácil de analizar mediante componentes de movimiento rectangulares.
Los componentes del movimiento
¿Qué sucede si el movimiento no tiene lugar a lo largo de un eje? Es decir, su movimiento no puede describirse en una sola dimensión. Se necesitan ambas coordenadas `x` y `y` para describir el movimiento.
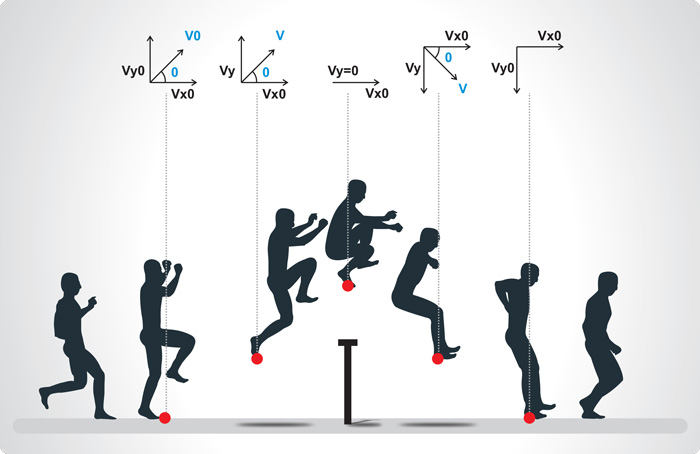
Los movimientos en dos dimensiones no son considerados en línea recta, quiere decir que se mueve simultáneamente a través de las dos direcciones.
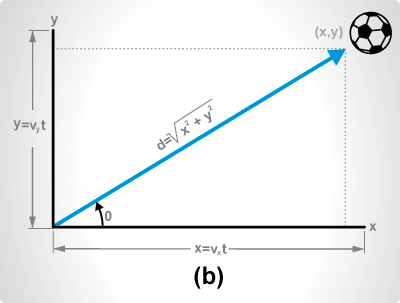
Empecemos considerando el comportamiento de la velocidad, tiene componentes tanto en `x` como en `y`. Recordemos que la velocidad es vectorial, por tal razón, tendría componente en `x` y en `y`.
`v_x = v cos theta`
`v_y = v sin theta`
`v = sqrt(v_x^2+v_y^2)` Magnitud del vector velocidad
Sin duda, ya se han utilizado antes componentes similares bidimensionales, en las componentes de longitud o desplazamiento, en el tiempo `t` está dada por:
`x = v_x t`
`y = v_y t`
Estas ecuaciones son para cuando la aceleración es cero.
Ecuaciones cinemáticas para las componentes del movimiento
Para el movimiento en el plano con aceleración constante que tiene componentes `a_x` y `a_y`, se establecen las siguientes ecuaciones:
`x = v_"x0"t + 1/2 a_x t^2`
`y = v_"y0"t + 1/2 a_y t^2`
`v_x = v_"x0" + a_x t`
`v_x = v_"y0" + a_y t`
Si un objeto se mueve con velocidad constante experimenta una aceleración (vector) en la dirección de la velocidad `(0°)` o en la opuesta `(180°)`, puede continuar en la trayectoria en línea recta, ya sea aumentando su velocidad o disminuyéndola, respectivamente.
Cuando el movimiento de un objeto es curvilíneo, se requiere aceleración, debido a que necesita variar la forma de la trayectoria. En este caso, la dirección del movimiento, varía con el tiempo, por lo que el movimiento no sigue una trayectoria recta.