Ecuaciones cinemáticas

Descripción cinemática del movimiento

Para describir el completamente el movimiento de los cuerpos, se debe conocer su posición en cualquier instante de tiempo. Entonces, nos podemos hacer la siguiente pregunta: ¿En qué posición se encuentra el cuerpo en cualquier instante de tiempo? Si la aceleración varía en el tiempo, la posibilidad de analizar dicho movimiento con estas características se vuelve muy complejo. Un caso simple, es aquel que se realiza en una dirección con aceleración constante. Si la aceleración es constante, significa que la velocidad cambia de manera uniforme en todo el movimiento.

Para la descripción del movimiento con aceleración constante, requiere de las siguientes ecuaciones básicas:

`x = bar v t`

`bar v = (v + v_0)/2`

`bar v = bar (v_0) + bar a t`

`x = bar (x_0)t + 1/2 bar a t^2`

`v^2 = v_0^2 + 2ax`

Ejemplo: Movimiento con aceleración constante

Caída libre

Uno de los casos más familiares de aceleración constante se debe a la gravedad cerca de la superficie de la Tierra. Cuando un objeto cae, su velocidad inicial es cero (en el instante en que es liberado), pero un tiempo después durante la caída, tiene una velocidad que no es cero. Ha habido un cambio en la velocidad y, por definición, una aceleración. La aceleración debida a la gravedad (g) tiene un valor aproximado (magnitud) de `g= 9,8 "m"/"s"^2`.

Ejemplo: Movimiento de caída libre

Los valores dados aquí para g son sólo aproximados pues la aceleración debida a la gravedad varía ligeramente en diferentes lugares como resultado de las diferencias en la elevación y la masa promedio regional de la Tierra.

Se dice que los objetos en movimiento solo bajo la influencia de la gravedad, están en caída libre. La aceleración debida a la gravedad g es la aceleración constante para todos los objetos en caída libre, sin considerar su masa ni su peso.

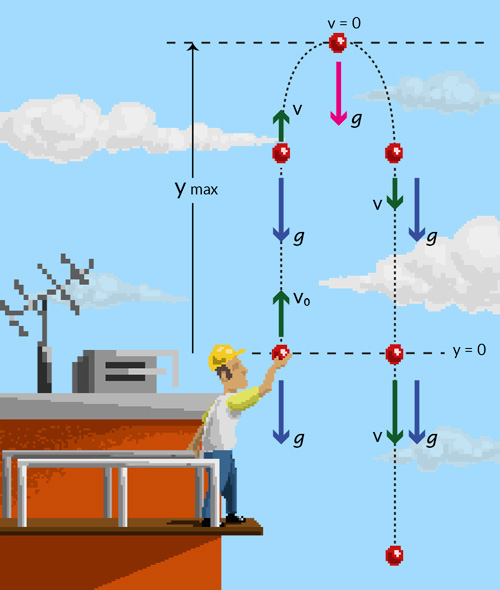
Para la descripción del movimiento de caída libre, se acostumbra utilizar y para representar la dirección vertical y tomar hacia arriba como positiva, y se requiere de las siguientes ecuaciones básicas:

`y = bar v t`

`bar v = (v + v_0)/2`

`bar v = bar (v_0) + bar g t`

`y = bar (y_0)t + 1/2 bar g t^2`

`v^2 = v_0^2 + 2gy`

Ejemplo: Trayectoria de la pelota

Actividades de aprendizaje

Movimiento con aceleración constante

Problema:

Observa en el siguiente ejemplo el procedimiento para resolver el problema.

Un bote de motor parte del reposo en un lago y acelera en línea recta a una velocidad constante de `3 "m"/"s"^2` durante `8"s"`. ¿Qué tan lejos viajó el bote durante ese tiempo?

`V_0= 0"m"/"s"`

`a= 3"m"/"s"^2`

`t = 8"s"`
Para determinar la magnitud del desplazamiento, primero se hace necesario conocer el valor de la velocidad final del bote, así:

`bar v = bar (v_o) + bar a t = 0+ (3 "m"/"s"^2 )(8"s")=24 "m"/"s"`
La velocidad media dentro de ese intervalo de tiempo es:

`bar v = (v + v_0)/2 = (24"m/s" + 0)/2 = 12 "m"/"s"`
Finalmente, la magnitud del desplazamiento o la distancia recorrida es:

`x = bar v t = (12"m/s")(8"s")= 96"m"`

Movimiento de caída libre

Problema:

Observa en el siguiente ejemplo el procedimiento para resolver el problema.

Un niño que está sobre un puente tira verticalmente una pelota hacia el rio abajo con una velocidad inicial de `25,4 "m/s"`. Si la pelota choca con el agua `4"s"` después, ¿Cuál es la altura del puente sobre el rio?

`V_0 = -25,4 "m/s"`
(Hacia abajo se toma como la dirección negativa)

`t=4"s"`

`g=9,8 "m"/"s"^2`
Consideremos las ecuaciones que nos darán la solución usando los datos dados, es evidente que la distancia que la piedra recorre en un tiempo t se da directamente por:

`y = bar (y_0)t + 1/2 bar g t^2 = (-25,4 "m/s")(4"s") -1/2(9,8"m"/"s"^2)(4"s")=104,1"m"`

El signo negativo indica que el desplazamiento es hacia abajo, lo cual concuerda con lo que se sabe de la formulación del problema.

Trayectoria de la pelota

Problema:

Observa en el siguiente ejemplo el procedimiento para resolver el problema.

Un trabajador está en un andamio frente a un anuncio y tira una pelota en línea recta hacia arriba. La pelota tiene una velocidad inicial de `21,2 "m/s"` cuando deja la mano del trabajador en el mismo nivel que la parte superior del anuncio.
1. ¿Cuál es la altura máxima que alcanza la bola medida desde la parte superior del anuncio?
2. ¿Cuánto tiempo le toma alcanzar esa altura?
3. ¿Cuál es la posición de la bola en `t = 3"s"`?
`V_0=21,2 "m/s"`

`g=9,8 "m"/"s"^2`

`v=0`

`t=3"s"`
a. Se observa que se refiere a la altura `(y=0)` de la parte superior del anuncio. Para esta parte solo debe preocuparnos del movimiento hacia arriba: la pelota se tira hacia arriba y se detiene a la altura máxima `y_"max"`.

`v^2 = v_0^2 + 2gy`

`v^2 = 0 + 2gy_"max"`

`y_"max" = (v^2)/(2g) = (21,2"m/s")^2/(2(9,8"m/s"^2))= 22,93"m"`
b. El tiempo que la pelota viaja hacia arriba para alcanzar la `y_"max"`:

`bar v = 0 = bar (v_0) + bar g t`

`t = bar (v_0)/g = (21,2 "m/s")/(9,8"m/s"^2) = 2,15"s"`
c. La altura de la pelota en `t =4"s"` está dada directamente por:

`y = bar (y_0)t + 1/2 bar g t^2 = (21,2"m/s")(4"s")-1/2(9,8"m/s"^2)(4"s")^2 = 6,4"m"`

Cuestionario

Instrucciones:

Seleccione la respuesta correcta y haz clic en el botón "Calificar" para obtener el puntaje de esta actividad.

Lección 2 Ecuaciones cinemáticas

Descripción cinemática del movimiento

Caída libre

Actividades de aprendizaje

Movimiento con aceleración constante

Problema:

Movimiento de caída libre

Problema:

Trayectoria de la pelota

Problema:

Cuestionario

Instrucciones:

Lección 2
Ecuaciones cinemáticas