Lección 1
Un cambio en el movimiento
La descripción del movimiento en varias dimensiones, señala la representación del universo sin reposo. Si usted está sentado, experimentando quietud, su silla, el edificio, y el aire que respira se mueven al mismo ritmo del movimiento de la Tierra.
Dentro del estudio de la física, la mecánica se encarga del estudio del movimiento, lo que lo produce y lo que lo afecta. La mecánica se divide en dos partes: CINEMÁTICA y DINÁMICA.

Para reflexionar:
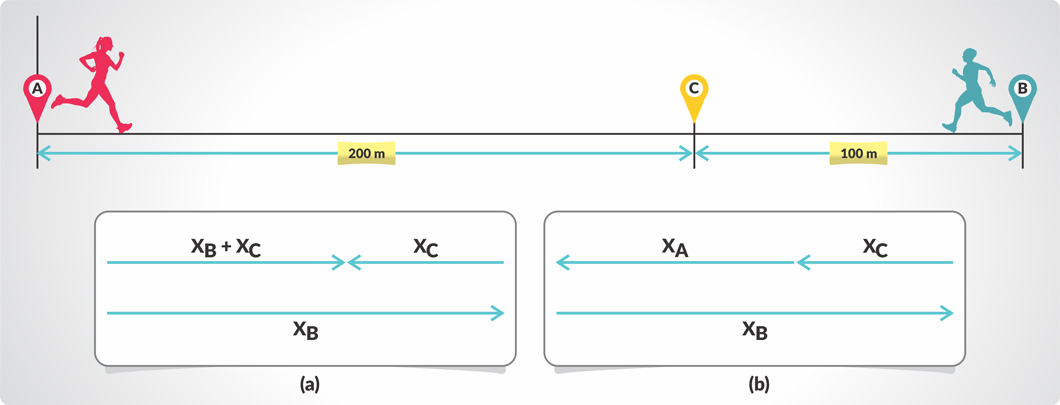
- ¿Puede ser cero el desplazamiento de un punto a otro, aunque la distancia entre estos dos puntos no sea cero?
- ¿Puede ser cero la distancia entre dos puntos, aunque el desplazamiento de uno a otro no sea cero?
- Si le dicen que un amigo camina 100m, ¿Puede decir con seguridad la posición final del amigo en relación al punto de inicio?
- ¿Es correcto decir, que el transportador espacial está acelerando cuando frena hasta detenerse?
- Si todos los fragmentos son expulsados con la misma rapidez, ¿con qué ángulo de expulsión caen más lejos del volcán?
Empecemos con la siguiente pregunta: ¿Qué es el movimiento? La respuesta a este interrogante parece sencilla, pero después de pensarlo con detenimiento, pueden surgir dudas de la manera más conveniente de contestarlo.
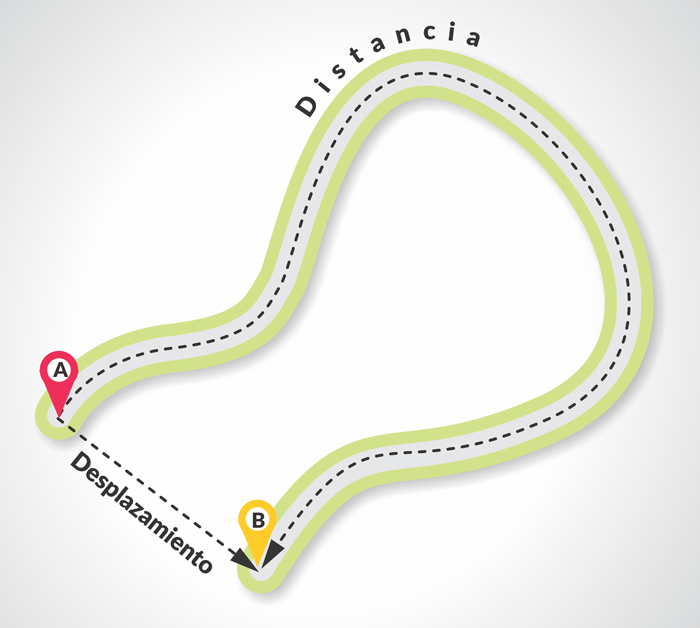
Se podrá concluir entonces, con qué movimiento solo es el cambio de posición. Ahora bien, si se puede mover de una posición o puntos a otros, la longitud total de la trayectoria recorrida se conoce como distancia.
Vectores y escalas
En física, se considera la distancia una cantidad escalar, solo tiene magnitud o valor numérico. Para cantidades vectoriales, están debe expresarse apoyados en la representación gráfica a través de los vectores. Son ejemplos de cantidades vectoriales: la representación de nuestro recorrido en avión como 56 km al norte (magnitud y dirección) se está dando la descripción vectorial, la velocidad y aceleración.
Desplazamiento
Al hablar del movimiento en una dimensión o en una línea recta, se necesita conocer claramente la posición, mediante la referencia a través de la utilización de sistemas coordenados, tales como el sistema cartesiano. Entonces, el desplazamiento se puede definir como una cantidad vectorial con magnitud y dirección y que describe una distancia en línea recta entre dos puntos.
Un desplazamiento lineal, se representa así:
`Delta X = x_2 -x_1`
Donde `x_1` y `x_2` son las posiciones inicial y final, respectivamente. El símbolo delta `Delta` significa diferencia o cambio en. El cambio en la posición que define el desplazamiento, está dado por signo (+ o - ) que determina la dirección del mismo.
Rapidez y velocidad
Rapidez y velocidad a veces se usan como sinónimos, pero son términos con significados diferentes. Básicamente, la rapidez es una cantidad escalar y la velocidad es una cantidad vectorial: tiene magnitud y dirección.
Al analizar el movimiento de los cuerpos, es necesario tener en cuenta, que su posición cambia con el tiempo. Es decir, se mueve cierta distancia en un tiempo dado. Lo anterior, puede expresarse utilizando longitud y tiempo para indicar el intervalo de tiempo del cambio de posición o rapidez de cada uno.
`"Rapidez promedio" = "distancia recorrida"/"tiempo total del recorrido" = (Delta d)/(Delta t)`
La unidad en el SI estándar para la rapidez es `m/s` (`"longitud"/"tiempo"`). La distancia es una cantidad escalar, al igual que el tiempo, por tal razón, la rapidez es una cantidad escalar.
Rapidez Instantánea es considerada cuando el intervalo de tiempo (`Delta t`) se hace cada vez menor y se aproxima a cero.
La velocidad nos dice que tan rápido y en qué dirección se mueve el cuerpo.
`"Velocidad promedio" = "desplazamiento"/"tiempo total" = (vec (Delta x))/(Delta t)`
`vec v = ( bar(Delta x) )/( Delta t) = (x - x_0)/(t - t_0)`
La diferencia de los vectores, `Delta x= x – x_0`, es sencillamente el desplazamiento entre las posiciones final e inicial. Los subíndices de `x_0`, `t_0` se usan para las condiciones iniciales del movimiento; mientras que los símbolos de `x`, `t` se usan para las condiciones finales.
Para el movimiento en una dimensión es conveniente utilizar los signos más o menos (+ o -) para indicar los sentidos del desplazamiento y las velocidades a lo largo de los ejes positivo y negativo. Cuando las condiciones iniciales son cero, las expresiones se simplifican así:
`bar v = ( bar(Delta x) )/( Delta t) = x/t`
Al igual que con la rapidez, cuando `Delta t` se aproxima a cero, se obtiene la velocidad instantánea, que describe que tan rápido y en qué dirección se mueve algo en un instante determinado. Entonces, La velocidad instantánea es un vector cuya magnitud es la rapidez instantánea. La dirección de dicho vector es la dirección del movimiento en ese instante particular.
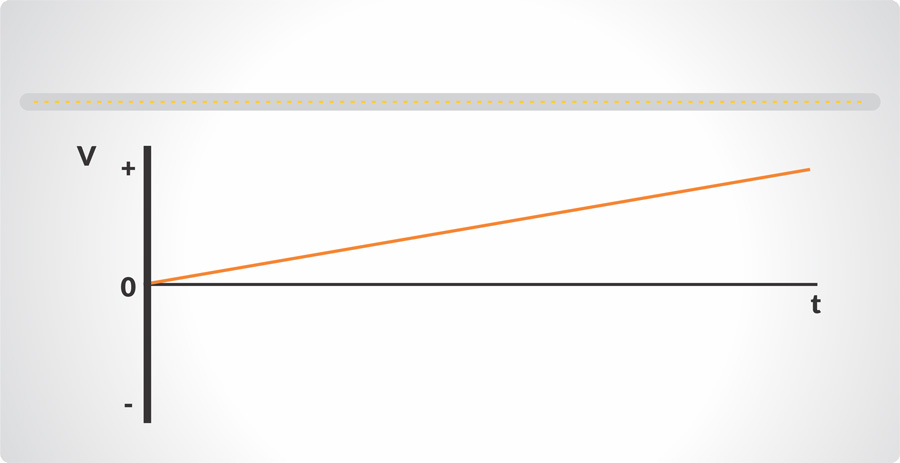
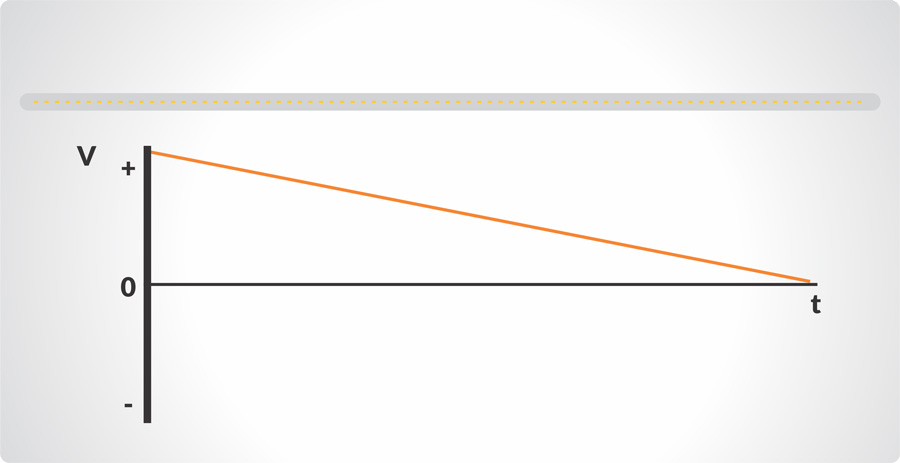
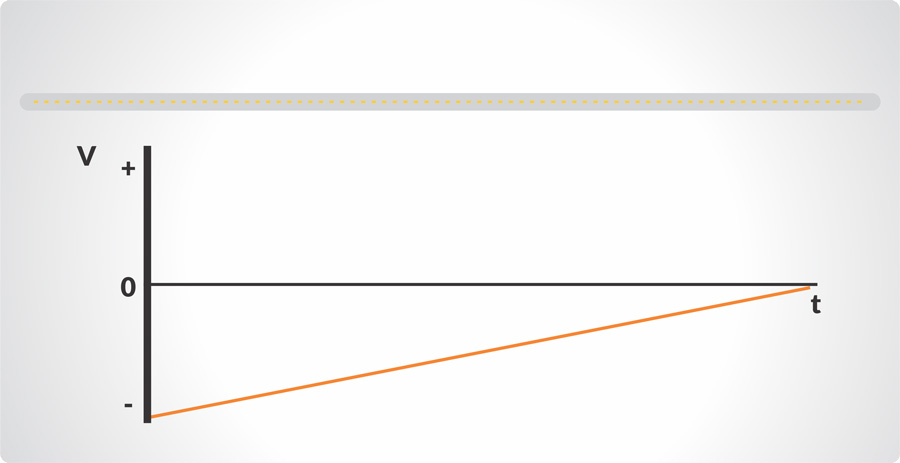
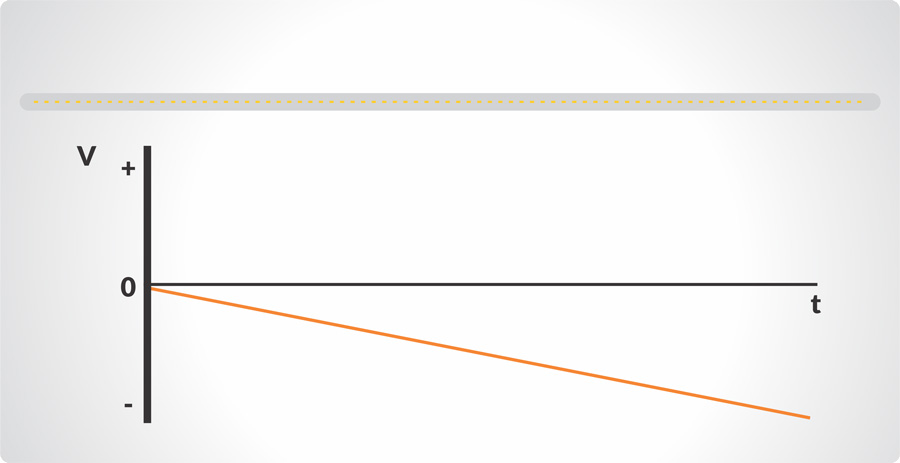
Aceleración
La descripción básica de un movimiento comprende el intervalo de tiempo de un cambio de posición, que puede expresarse por la velocidad. Supongamos que algo se está moviendo a una velocidad constante y que la velocidad cambia; esto es una aceleración. Análoga a la velocidad promedio es la aceleración promedio, o el cambio de velocidad dividido entre el tiempo que tomó dicho cambio. Así mismo, la aceleración instantánea es análoga a la velocidad instantánea, siendo definida como la aceleración en un instante determinado.
`"Aceleración promedio" = "cambio de velocidad"/"tiempo para hacer el cambio"`
`vec a = ( bar(Delta v) )/( Delta t) = (v - v_0)/(t - t_0)`
Las dimensiones de la aceleración son `"longitud" / ("tiempo"^2 )`. Las unidades SI para la aceleración son por consiguiente `"m"/"s"^2`.
Dado que la velocidad es una cantidad vectorial, que tiene tanto magnitud como dirección, un cambio en la velocidad puede afectar a uno o ambos factores. Por consiguiente, una aceleración puede ser el resultado de un cambio en la rapidez (magnitud), un cambio en la dirección, o un cambio en ambas.