Lección 3
Aplicaciones de las leyes de Newton
Diagramas de cuerpo libre (D.C.L)
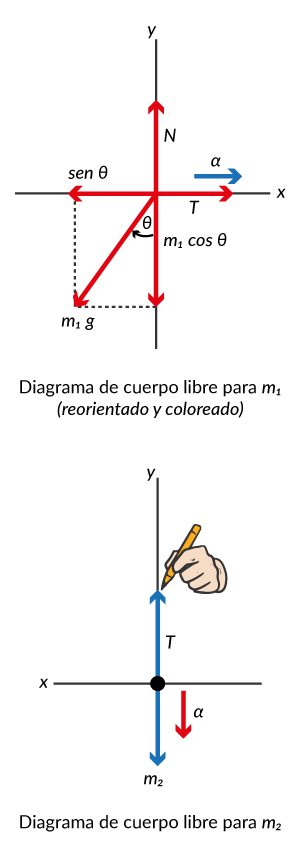
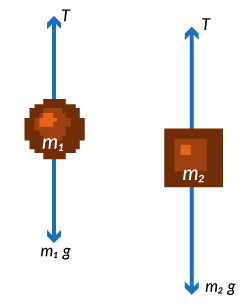
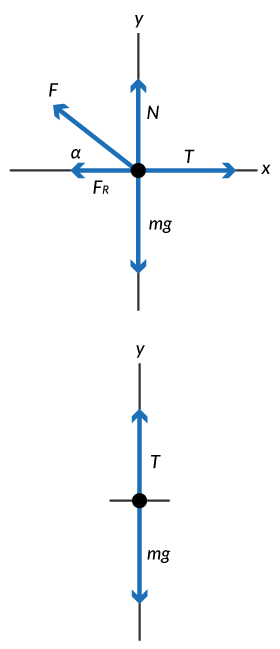
Cuando se trabaja con problemas en los que dos o más fuerzas o componentes de una fuerza actúan sobre un cuerpo, es conveniente e instructivo dibujar un diagrama del cuerpo libre con las fuerzas. Se debe ilustrar mediante la aplicación de diagramas de cuerpo libre, donde se muestran todas las fuerzas que actúan sobre un cuerpo u objeto. Si están comprendidos varios cuerpos, se puede hacer un diagrama separado para cada cuerpo, buscando mostrar de forma individual todas las fuerzas que actúan sobre cada cuerpo.
Sobre este esquema se elige un sistema de referencia conveniente para aplicar las leyes de Newton. Cuando se considera un sistema mecánico con varios cuerpos, se debe hacer el diagrama de cuerpo libre y aplicar las leyes de Newton para cada componente del sistema. La fuerza que produce una superficie sobre un cuerpo que se encuentra apoyado en la superficie se llama fuerza normal N, las fuerzas que ejercen cuerdas y cables sobre un cuerpo se llaman fuerza de tensión T.
A menos que se diga lo contrario, las cuerdas y poleas que formen parte de un sistema mecánico se considerarán de masa despreciable comparada con la masa de los cuerpos en estudio y las cuerdas y cables se considerarán inextensibles, esto significa que sirven sólo para cambiar la dirección de la tensión cuando pasan por una polea; se dice que son ideales.
En resumen, los pasos generales son los siguientes:
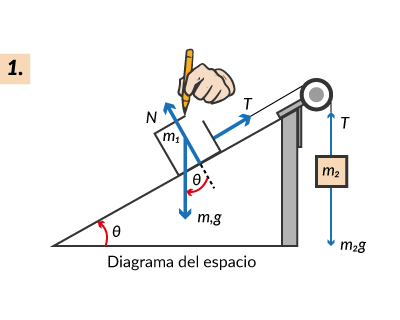
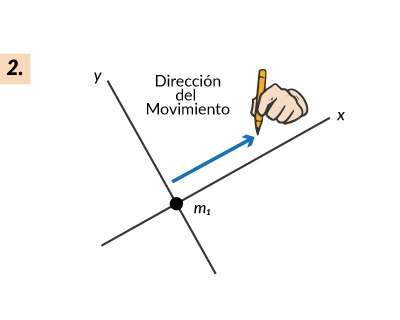
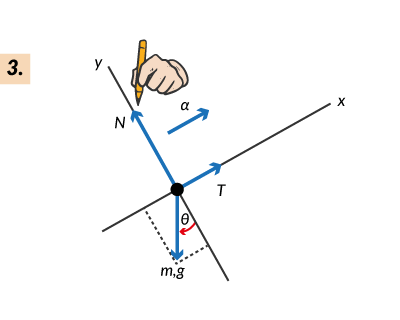
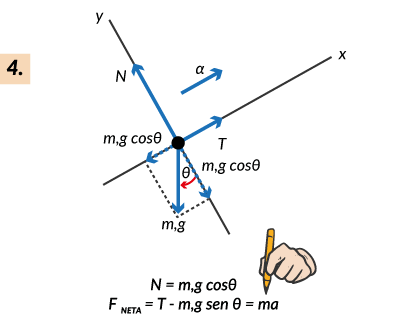
Fricción
La fricción se refiere siempre a la resistencia presente en el movimiento que ocurre cuando dos materiales o medios, están en contacto uno con el otro. Esta resistencia ocurre para todos los tipos de medios: sólidos, líquidos y gaseosos, y se caracteriza como la fuerza de fricción.
La fricción entre sólidos se clasifica por lo general en tres tipos: estática, deslizante (cinética) y de rotación. La fricción estática ocurre en todos los casos, en los que la fuerza friccional es suficiente para evitar el movimiento relativo entre superficies. La fricción cinética o fricción deslizante ocurre cuando hay un movimiento relativo (de deslizamiento) en la interfase de las superficies en contacto. La fricción de rotación ocurre cuando una superficie rota en lugar de deslizarse o resbalarse en el punto o área de contacto con otra superficie.
`F_"R" = µN`
- `F_"R"`: Fuerza de fricción
- µ: Coeficiente de fricción
- N: Fuerza normal
Actividades de aprendizaje
Bibliografía
- Wilson, Jerry D. Física. Segunda edición. Ed. Pearson Educación. 1996. ISBN 968-880-660-9
- Serway, Raymond y Jewet, John. Física I. Tercera edición. Texto basado en Cálculo. Ed. Thomson. 2004. ISBN 970-686-339-7
- Sears, Zemansky, Young, Fredman. Física Universitaria. Undécima edición.Person Ed.